Geodesic Calculus on Latent Space

Introduction

In “Geodesic Calculus on Latent Spaces” by Hartwig et al., they propose a practical Riemannian toolkit for deep generative models: learn a projection onto the data manifold that lives inside a model’s latent space, and then use it to compute geodesics, exponential maps, and related operators in a numerically robust way.

Latent spaces of autoencoders and VAEs are not flat Euclidean clouds; around the data they behave like curved manifolds. Linear interpolation cuts through “holes” (low-density regions), often producing blurry or invalid samples. The paper shows how to build a reliable geometric calculus inside latent space, so we can move along the manifold: shortest paths (geodesics), shooting via exponential maps, etc., without requiring perfectly accurate decoders or explicit charts. This extends a growing line of work on the Riemannian view of deep generative models (The Riemannian Geometry of Deep Generative Models, Shao et al.)

The core idea is to treat the true data manifold as an implicit submanifold of the ambient latent space and learn a projection $\Pi$ onto it (via denoising); then perform discrete Riemannian calculus by repeatedly stepping in latent space and projecting back onto the manifold.

Mathematical essentials

• Manifold in latent space. Let $Z\subset\mathbb{R}^m$ be the ambient latent space of an autoencoder, and $\mathcal{M}\subset Z$ the (unknown) subset carrying the data distribution $E(x)\in \mathcal{M}$. We do not parameterize $\mathcal{M}$ explicitly; we only assume access to samples near it.

• Projection $\Pi$. Learn a map $\Pi:Z\to Z$ with $\Pi(z)\approx z$ for $z\in\mathcal{M}$ and $\Pi(z)\in\mathcal{M}$ for noisy/off-manifold $z$. A simple training objective is denoising:

  $$\min_\Pi\ \mathbb{E}_{z\sim E(x),\ \varepsilon\sim\mathcal N(0,\sigma^2I)} \big|\Pi(z+\varepsilon)-z\big|^2,$$

  which encourages fixed-point $(\Pi(z)\approx z)$ and idempotence $(\Pi(\Pi(z))\approx \Pi(z))$ properties typical of projections. This is the key robustness lever of the paper.

• Discrete geodesic energy. For a path $\gamma=(\gamma_0,\ldots,\gamma_K)$ with endpoints $\gamma_0=z_a,\ \gamma_K=z_b$,

  $$E(\gamma)=\sum_{k=0}^{K-1}|\gamma_{k+1}-\gamma_k|^2$$

  approximates squared length. The algorithm alternates gradient steps on $E$ in $Z$ with projections $\gamma_{1:K-1}\leftarrow \Pi(\gamma_{1:K-1})$. The projection enforces manifold feasibility; the gradient tries to shorten the curve, together yielding a discrete geodesic. (Regularizers can keep $\gamma$ near the VAE prior.)

• Exponential map / shooting. With $\Pi$, one can numerically realize the exponential map $\exp_p(v)$ by short projected steps starting at $p$ in an initial direction $v$, enabling “shooting” of geodesics from a point.

This “project–optimize–project” pattern does not require a perfect decoder metric or explicit tangent frames, only a good projection.

What the experiments show

Across synthetic and real datasets (with different autoencoders), the learned $\Pi$ yields:

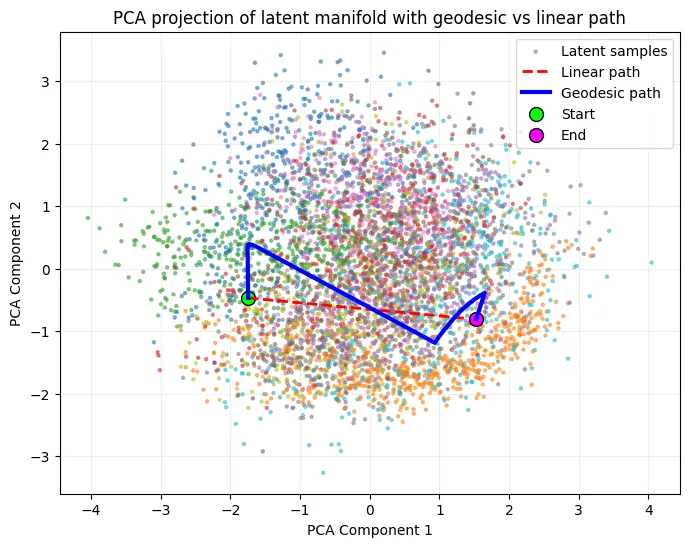
• Smooth, valid interpolations: projected geodesics stay in high-density latent regions; decoded frames are crisp and semantically consistent, unlike linear latent blends that traverse holes.
• Robust calculus: geodesic paths and exponential shooting remain stable even when the manifold is only approximately represented.

How it compares

• Versus linear latent interpolation: linear paths are cheap but ignore curvature/topology; they often decode to implausible images mid-way. The paper’s geodesics are longer (because they bend around holes) but faithful to the data manifold.
• Versus explicit Riemannian metrics: previous work builds metrics from decoder Jacobians; accurate but brittle and costly. Here, $\Pi$ externalizes manifold knowledge and makes calculus projection-based, which is numerically simpler and decoupled from the decoder.

Where to use it

• Generation and editing: semantically consistent morphing (e.g., pose or identity changes) and “move along the manifold” operations.
• Representation learning: geometry-aware distances and retrieval along geodesics instead of Euclidean shortcuts.
• Robotics / motion planning: learned manifolds of feasible states with geodesic skills.

A minimalist recipe

1. Train an encoder-decoder (VAE/AE) on your data.
2. Collect latent codes $z=E(x)$ and train a small MLP $\Pi$ with the denoising loss above; optionally add fixed-point/idempotence penalties.
3. Geodesic between $(z_a,z_b)$: initialize $\gamma$ linearly; iterate (i) gradient descent on discrete energy $E(\gamma)$ in $Z$, (ii) project internal nodes with $\Pi$; clamp endpoints.
4. Decode the path to visualize a geometry-aware interpolation.

Experiments

The experiments conducted in this notebook translate the theoretical framework of the paper into a concrete implementation on the MNIST dataset.

A VAE was first trained to learn a structured 16-dimensional latent representation of handwritten digits, where proximity between points reflects visual similarity. On top of this learned manifold, a projection network $\Pi$ was trained as a denoising operator that maps any noisy or off-manifold latent code back toward the manifold of valid encodings, effectively approximating the Riemannian projection operator described in the paper.

Using $\Pi$, we computed discrete geodesic interpolations between latent representations of two digits (for example, “2 → 9”) by iteratively optimizing a path to minimize its energy while keeping each intermediate point projected onto the manifold. The resulting geodesic paths produced smoother, semantically coherent digit transitions than conventional linear interpolations.

Finally, PCA visualizations of the latent space revealed that the learned geodesic trajectories bend through dense data regions, faithfully following the manifold’s intrinsic geometry rather than cutting across low-density zones. These results empirically confirm the paper’s core idea: that a learned projection operator can endow deep latent spaces with a consistent geometric structure, enabling manifold-aware interpolation and analysis.